最近对状态机产生了兴趣。看了老外的文章才知道这个领域真是旷阔无边,他们做学问的态度实在是扎实。所以先做个读书笔记。
状态机的性能指标太多,我能力有限,目前在考察范围内的只有所需的逻辑资源和简单的时序特性两项指标。
影响一个状态机的性能有多个因素,包括状态集合的编码、状态机的HDL编写方式、所采用的器件结构,以及其他应用相关的因素。
________________________________________
• 状态编码
常见的状态编码包括顺序二进制编码、one-hot及改进的one-hot编码、Gray码等。
顺序二进制编码,即将状态依次编码为顺序的二进制数。顺序二进制编码是最紧密的编码,优点在于它使用状态向量的位数最少。例如 对于6个状态,只需要3位二进制数来进行编码,因此只需要3个触发器来实现,节约了逻辑资源。(在实际应用中,往往需要较多组合逻辑对状态向量进行解码以产生输出,因此实际节约资源的效果并不明显。)
在上面的例子中,3位二进制数总共有8种可能的编码模式,其中6种用来表示有效状态,剩下的2种是无效编码。
有人认为顺序二进制编码还有一个好处。当芯片受到粒子辐射或者由于异步输入等问题可能会造成状态跳转失常。如果失常中状态机跳转到无效的编码状态则可能会出现死机,除非复位否则永远无法回到Idle状态。因为顺序二进制编码最紧密,所以无效编码最少。失常时有更大的概率跳转到的有效状态,并最终回到Idle状态。
这种预想的好处并不会发生在实际中。首先,失常的跳转到有效状态并不意味着能够最终回到Idle状态。例如在某个有效状态,状态机循环等待某输入信号,并作出应答。如果状态机失常的跳转到该状态,同样会陷入死等,因为输入信号并不会到来。其次,失常的跳转到有效状态,意味着可能在不正确的时机产生输出,这样会将故障传播到其他模块。在很多应用中人们宁愿死机不输出任何信号也不愿意输出错误的信号。
可见使用顺序二进制编码并不能使得状态机具有所想象的容错能力。
在上面提高的失常跳转情况下,one-hot编码往往工作得更好。有趣的是,它恰恰是最不紧密的编码。
在one-hot编码中,对于任何给定状态,状态向量只有1位置1,所有其它的状态位都为0。one-hot编码最长,因为n个状态就需要n位的状态向量。
one-hot编码的状态机最大的优势是它的速度。one-hot状态机的速度与状态的数量无关,仅仅取决于到某特定状态的跳转的数量。而相对的,状态增加时使用顺序二进制编码的状态机速度会急剧下降。
one-hot编码其他的优点还有易于综合、易于寻找关键路径、易于进行静态时序分析等。具体来说,要判断当前是否在某一状态,只需要判断状态向量的对应位是1还是0即可。考虑一个典型的输出,它在某些状态输出1,剩下的状态输出0。只需要将状态向量中的对应位OR起来即可产生该输出。也就说输出很容易产生,并且从状态稳定到输出稳定的延时很确定(一个OR门的延时),因此易于综合以及进行静态时序分析。
应当注意的是one-hot编码有很多无效状态,因此在编写状态机时应该确保一旦进入无效状态可以立即跳转到确定的已知状态(通常是Idle)。(简单的说就是生成下一状态的case语句要加default;或者在case之前先赋上默认值,到case里再覆盖。)
当发生失常跳转时one-hot编码有很大的概率跳转到无效状态,而它的无效状态现象很明显(比如将状态向量都接到灯上,一旦同时亮多个灯就表明工作失常),即使不加处理也很容易被外部逻辑检测到,从而可以说是易于调试的。
one-hot状态机有很多变体。比如将Idle状态编码为0,其他状态按照正常的one-hot编码。即对于除Idle外的每个给定状态,对应的状态向量中有1位置1,其他位为0。这种变体的好处是在复位时可简单的将状态向量的各个触发器清0。
另一种常见的变体称为"almost one-hot"编码。假设状态机有功能几乎相同的两组状态(例如,处理对某设备的读访问和写访问),可以使用1个状态位来指示状态机当前正处在两组状态中的哪一组,而剩下的状态位采用普通的one-hot编码。(例如一组状态为4'b0001, 4'b0010, 4'b0100,另一组为4'b1001, 4'b1010, 4'b1100。)因此要对给定状态进行完整的解码需要考察两个状态位。这种机制具有使用纯one-hot编码的大多数好处,但逻辑更小。
one-hot状态机有一个缺点,它的状态每次发生跳转,所有的状态位都会发生变化。首先,状态机的输出往往是由状态位组合生成的。同时变化的状态位越多,组合输出稳定前所需的时间就越长,产生的毛刺就越多。如果该输出不经同步就直接连接到寄存器的时钟、使能、或锁存器的使能等控制端口,将很容易导致数据的破坏。(正统解决方案是加一级寄存器来同步状态机的输出,该方案可能会产生一个周期的延迟,而且如果该输出稳定前所需的时间过长还是会违背寄存器的建立时间。)其次,对于有异步输入的系统,在时钟沿到来时有多个状态位发生变化,即有多个寄存器可能受异步输入的影响,使得亚稳态发生的概率有所增加。(虽然这并不是one-hot编码的问题,根本的解决方案还是避免异步输入。)
因此,有些工程师使用Gray码的状态机来解决上面的问题。
Gray码状态机在发生状态跳转时,状态向量只有1位发生变化。理论上说Gray状态机在状态跳转时不会有任何毛刺。但是实际上综合后的状态机是否还有这个好处也很难说。Gray码状态机设计中最大的问题是,在状态机很复杂状态跳转的分支很多时,要合理的分配状态编码保证每个状态跳转都仅有1位发生变化,这是很困难的事情。
(总结的说,在小设计中可以考虑使用Gray码或one-hot。大设计中,由于现在技术进步几乎不用考虑逻辑资源不够的问题,可以考虑使用one-hot编码以提高速度。至于顺序二进制编码,一般不予考虑。但是要达到最佳性能,需要使用更高级的编码算法,针对给定的状态机进行分析。)
有不少学者对状态编码展开了深入的研究工作,并对于给定状态机的编码优化提出了多种算法。比如有一种算法,目的是使得描述组合输出的逻辑表达式中的项与文字的数量最小,以减少组合输出电路中的门。这些方法有一些基本概念是共同的,如下。
令S为有限集合(在状态编码问题中S表示FSM的状态集合)。
二分法(或者翻译成二元组?)(l,r)是一对不相交的S的子集。这两个子集分别称为左块(或0块)和右块(或1块)。二分法定义了一个一位二进制编码的变量,它的值随状态变化,对于左块中的状态将该变量取值0,对于右块中的状态该变量取值1。对于不包含在左块和右块中的状态,该变量取值为don't-care。这样,由b个二分法组成的集合,定义了长度为b的编码,编码中可能有不完全确定的位(即无关位)。
二分法(l,r)定义的状态变量代表了l中的状态与r中的状态的差别,二分法表达的信息可以表示为信息集合IS((l,r))={si/sj|si∈l∧sj∈r}。si/sj称为原子信息。表达原子信息si/sj的二分法({si},{sj})称为原子二分法。原子二分法代表了状态si和状态sj的差别。
两个二分法(l1,r1)和(l2,r2)称为一致的,当且仅当l1∩r2=Φ∧r1∩l2=Φ(直接一致)或者l1∩l2=Φ∧r1∩r2=Φ(反转一致)。两个直接一致(反转一致)的二分法可以合并成新的二分法(l1∪l2,r1∪r2)((l1∪r2,r1∪l2))。
例如,3个二分法({a},{c})、({d},{a,b})、({a,c},{b,d})定义了集合S={a,b,c,d}的一个3位编码。前两个二分法是反转一致的,可以合并成二分法({a,b},{c,d})。这样就定义了集合S的新的2位编码。
|
状态 |
({a},{c}) |
({d},{a,b}) |
({a,c},{b,d}) |
|
a |
0 |
1 |
0 |
|
b |
- |
1 |
1 |
|
c |
1 |
- |
0 |
|
d |
- |
0 |
1 |
|
状态 |
({a,b},{c,d}) |
({a,c},{b,d}) |
|
a |
0 |
0 |
|
b |
0 |
1 |
|
c |
1 |
0 |
|
d |
1 |
1 |
基于二分法的状态编码思路如下:首先给各状态符号分配种子编码。根据种子编码,将下一状态和输出都表示为二分法定义的状态变量(即状态和输入的函数)。然后一步一步将这些状态变量合并,最终是使得成本函数COST最小。COST=sum(|sup(Yt)|),对于一切Yt∈Y,其中Y是FSM的下一状态和输出函数的集合,sup(Yt)是函数Yt的支持(Yt依赖的当前状态和输入)。
找到合适的一致的状态变量加以合并,使得成本函数最小,这是一个Np-hard问题。因此常采用启发式算法来实现。
例子如下。考虑一个状态机,它有2个输入i1,i2,1个输出o1,4个状态s1, s2, s3, s4。状态转移关系如下:
i1 i2 state nextstate o1
- 0 s1s10
1 1 s1s10
0 1 s1s2-
0 - s2s21
1 1 s2s10
1 0 s2s31
1 - s3s31
0 0 s3s21
0 1 s3s41
0 - s4s41
1 1 s4s31
种子编码采用所有原子二分法定义的编码,对于n个状态,需要n(n-1)位的编码。这些编码的每一位,表示相应的两个状态之间的差别,如下:
state s1/s2 s1/s3 s1/s4 s2/s3 s2/s4 s3/s4
s1000---
s21--00-
s3-1-1-0
s4--1-11
使用这种编码后的状态转移关系如下:
cubes x1x2y1y2y3y4y5y6 Y1Y2Y3Y4Y5Y6Y7
c1=- 0 0 0 0 - - -0 0 0 - - - 0
c2=1 1 0 0 0 - - -0 0 0 - - - 0
c3=0 1 0 0 0 - - -1 - - 0 0 - -
c4=0 - 1 - - 0 0 -1 - - 0 0 - 1
c5=1 1 1 - - 0 0 -0 0 0 - - - 0
c6=1 0 1 - - 0 0 -- 1 - 1 - 0 1
c7=1 - - 1 - 1 - 0- 1 - 1 - 0 1
c8=0 0 - 1 - 1 - 01 - - 0 0 - 1
c9=0 1 - 1 - 1 - 0- - 1 - 1 1 1
c10=0 - - - 1 - 1 1- - 1 - 1 1 1
c11=1 1 - - 1 - 1 1- 1 - 1 - 0 1
其中把当前状态和输入作为自变量(状态),下一状态和输出作为因变量(状态变量)。x1x2分别对应i1i2,y1~y6对应当前状态的6个编码位,Y1~Y6对应下一状态的6个编码位,Y7对应o1。c1~c11对应11种自变量组合模式。
目标是使各个状态变量的支持数量之和最小。现考察Y1的支持。Y1对应的二分法为({c1,c2,c5},{c3,c4,c8}),即Y1在c1,c2,c5模式中输出0,在c3,c4,c8模式中输出1,其他模式的输出不关心。这两组模式间的差别表示为原子二分法为c1/c3, c1/c4, c1/c8, c2/c3, c2/c4, c2/c8, c5/c3, c5/c4, c5/c8。建立如下矩阵。矩阵中的元素表示它所在行对应的模式分量是否对它所在列对应的模式差别产生影响。例如第1行第1列,表示x1是否对c1与c3的差别产生影响。在例子中x1在c1中为-,c3中为0,表示x1不对c1和c3的差别产生影响(即在x1这一分量上,c1与c3并没有不同),所以矩阵中的对应位为0。
c1/c3 c1/c4 c1/c8 c2/c3 c2/c4 c2/c8 c5/c3 c5/c4 c5/c8
x1 000111111
x2100001001
y1010010100
y2001001000
y3000000000
y4000000001
y5000000000
y6000000000
将该矩阵重新排序,使得每行包含的1的数量从大到小,每列包含的1的数量从小到大,如下:
c1/c3 c1/c4 c1/c8 c2/c3 c5/c4 c2/c4 c5/c3 c2/c8 c5/c8
x1 000111111
x2 100000011
y1 010001100
y2 001000010
y4 000000001
y3 000000000
y5 000000000
y6 000000000
从矩阵中很容易看出,对Y1产生影响的分量为x1, x2, y1, y2, y4,其中前四个分量就足以覆盖所有的列(即覆盖了所有Y1的原子二分法),因此y4为冗余分量可以排除,所以Y1的支持sup(Y1)={x1, x2, y1, y2}。
用同样的方法计算出所有状态变量的支持:
sup(Y1)={x1, x2, y1, y2}
sup(Y2)={x2, y1, y2, y3, y4, y5}
sup(Y3)={x1, y2, y3}
sup(Y4)={x1}
sup(Y5)={x2, y2, y3, y4, y5, y6}
sup(Y6)={x1}
sup(Y7)={x1, x2, y1, y2, y3, y4, y5}
然后考虑在y1~y6中合并两个一致的状态变量。
优先考虑在以上支持集合中出现次数最多的变量对。例如y1与y2这一对变量,在sup(Y1), sup(Y2), sup(Y7)这3个支持集合中出现。同样出现3次的还有(y2,y3), (y2,y4), (y2,y5), (y3,y4), (y3,y5), (y4,y5)。因此选择变量对进行合并时优先考虑合并这些变量。在上面这7对变量中选择一对进行合并,并计算合并后的支持集合中所含元素的个数之和,使得该和最小(万能的方式是逐一尝试)。这样就完成了第一步合并。反复多次合并,直到不能合并(找不到一致的变量对)为止。最后的得到的变量集合对应的二分法集合定义的编码即目标编码。
-
热敏电阻温度阻值查询程序2024年11月13日 74
-
C99语法规则2024年11月16日 675
-
FreeRTOS 动态内存管理2024年11月12日 448
-
一款常用buffer程序2024年11月06日 88
-
1602液晶显示模块的应用2012年08月03日 191
-
GNU C 9条扩展语法2024年11月18日 261
-
如何实现STM32F407单片机的ADC转换2024年11月15日 300
-
STM32使用中断屏蔽寄存器BASEPRI保护临界段2024年11月15日 195
-
C99语法规则2024年11月16日 675
-
51单片机LED16*16点阵滚动显示2012年09月05日 664
-
FreeRTOS 动态内存管理2024年11月12日 448
-
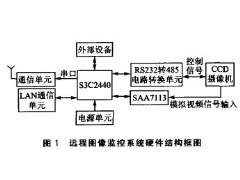
ARM9远程图像无线监控系统2012年07月03日 424
-
用单片机模拟2272软件解码2012年09月06日 300
-
如何实现STM32F407单片机的ADC转换2024年11月15日 300
-
新颖的单片机LED钟2012年08月06日 278
-
GNU C 9条扩展语法2024年11月18日 261