欧姆定律是电路分析与计算的基础。除了欧姆定律,电路分析与计算还离不开基尔霍夫电流定律和电压定律。电流定律应用于对电路结点的分析,电压定律应用于对电路回路的分析。 就图1.1 17电路,介绍支路、结点和回路的概念。
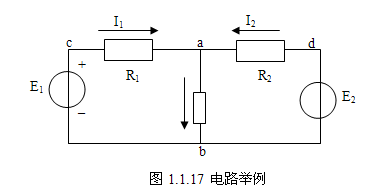
(1)支路:简单地说,电路中通过同一电流的分支称为支路。图1.1.17电路中有acb、adb和ab三条支路。其中,acb、adb支路中有电源,叫含源支路;ab中无电源叫无源支路。
(2)结点:电路中三条及三条以上支路的连接点叫结点。图1.1.17电路中,共有a、b两个结点,c和d不是结点。
(3)回路:由一条或多条支路组成的闭合路径叫回路。在图l 1 17电路中,共有三个回路: abca、adba、cbdac。
1.5.1基尔霍夫电流定律(KCL)
基尔霍夫电流定律是用来确定连接在同一结点上的各个支路电流之间的关系。 “电路中任何一个结点,所有支路电流的代数和等于零”,这就是基尔霍夫电流定律基本内容。电流的正负号通常规定为:参考方向指向结点的电流取正号,背离结点的电流取负号。
例如,图1.1.17电路中结点a( 图1.1.18所示)流经的电流可以表示为:
I1+I2 = I3 (1.5.1)
或将上式表示为
I1+I2 – I3 = 0
即 ∑I=0 (1.5.2) 电流定律
从上面的分析,基尔霍夫电流定律也可描述为:任何时刻,流入任一结点的支路电流等于流出该结点的支路电流,见式(1.5.1)。
基尔霍夫电流定律也可推广应用于包围几个结点的闭合面,图1.1.19所示电路中,闭合面S内有三个结点A、B、C。
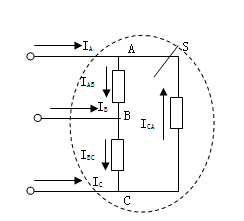
图1.1.19
由电流定律可列出
IA = IAB – ICA
IB = IBC – IAB
IC = ICA – IBC
﹡KCL为“Kirchhoff’s Current Law”的缩写;常用KCL代表基尔霍夫电流定律。
上面三式相加,得:
IA+IB+IC=0
即 ∑I=0
可见在任一时刻,通过任何一个闭合面的电流代数和也恒为零。它表示着流入闭合面的电流和流出闭合面的电流是相等的。基尔霍夫电流定律体现了电流的连续性。
1.5.2基尔霍夫电压定律(KVL)
基尔霍夫电压定律是用来确定回路中的各段电压间的关系。 “在任一回路中,从任何一点以顺时针或逆时针方向沿回路循行一周,则所有支路或元件电压的代数和等于零”,这就是基尔霍夫电压定律的基本内容。为了应用KVL,必须指定回路的参考方向,当电压的参考方向与回路的参考方向一致时带正号,反之为负号。
例如,图1.1.20回路cadbc,回路中电源电动势、电流和各段电压的参考方向均已标出。按虚线所示的回路参考方向可列出方程式
Ubc + Uca + Uad+ Udb = 0
即U1 + U2 + U3 + U4 = 0
也就是 ∑U=0 (1.5.3)
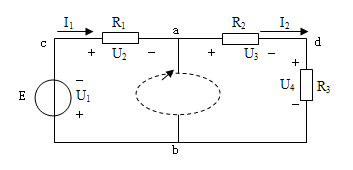
图1.1.20所示回路是由电动势和电阻构成的,因此上式也可表示为
E + R1I1 + R2I2 + R3I2 = 0
E = - R1I1 - R2I2 - R3I2
∑E=∑(RI) (1.5.4)
式(1.5.4)表示:任一回路内,电阻上电压的代数和等于电源电动势的代数和。电动势正负号的选定通常规定为参考方向与所选回路循行方向相反时取正号,一致时取负号;电流的参考方向与所选回路循行方向一致时,电阻上电压降取负号,相反时电压降取正号。
﹡KVI为“Kirchhoff’s Voltage Law”的缩写;常用KVL代表基尔霍夫电压定律。
基尔霍夫电压定律不仅适用于闭合回路,也可以推广应用到回路的部分电路,用于求回路中的开路电压。例如图1.1.21电路,求Uab。
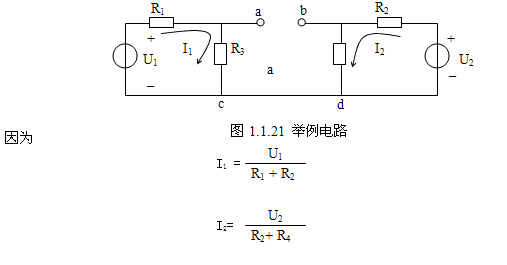
对回路acdb,由基尔霍夫电压定律得:
Uab + I2R4 - R3I1 = 0
则Uab = I1R3 ― I2R4
【例1.5.1】 如图1.1.22电路中,已知IA =1 mA,IB =10 mA,IC =2 mA,求电流Id?
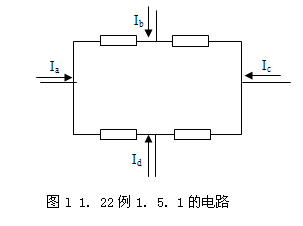
【解】根据基尔霍夫电流定律的推广应用,流人图示的闭合回路的电流代数和为零,即
IA+IB+IC+Id =0
所以
Id = -(IA+IB+IC)
=-(1+10+2) =-13 mA
【例1.5.2】 如图1.1.23一闭合回路,各支路的元件是任意的,已知:Uab=10 V,Ubc =一6 V,Uda =一5 V。求:Ucd和Uca。
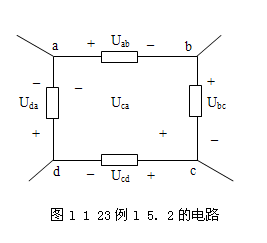
【解】
由KVL可列出下式
Ubc + Uca + Uad+ = 0
得 Uad = - Ubc - Uca - Udb
则 Uad =一10一(一6)一(一5)=1 V
若abca不是闭合回路,也可用KvL得
Ubc + Uca + Uca = 0
Uca =一10一(一6) = -4V
【练习与思考】
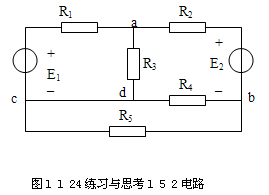
1 5 l 简述基尔霍夫电流定律和电压定律的基本内容。 图l l 24练习与思考l 5 2电路
I 5 2 试用基尔霍夫定律,列出图1 l 24所示电路中的各结点和回路的电流方程式、电压方程式。
-
一款高温报警电路2024年11月13日 81
-
可燃气体全自动点火器2012年09月22日 76
-
LED参数与特性2012年09月18日 118
-
RC振荡电路的几种接法2012年09月10日 221
-
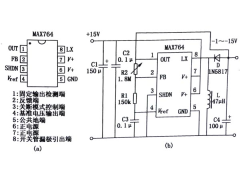
MAX764极性反转电路2012年08月24日 47
-
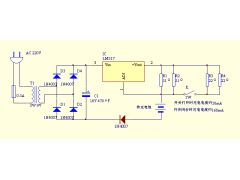
实用恒流充电器2012年08月18日 175
-
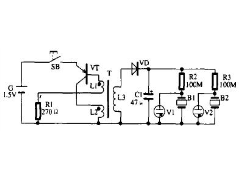
电子催眠器制作2012年08月15日 72
-
多普勒自动电子开关2012年08月02日 78
-
常用物质金属非金属的电阻率、导电率明细表2024年11月23日 4876
-
自制微型交流电焊机2012年07月14日 1143
-
声光控延时开关的制作2024年07月06日 915
-
用LM1875替找TDA20302012年09月15日 777
-
6N3+LM4780功放制作2012年09月13日 653
-
小型太阳能供电板的制作2012年09月08日 649
-
简单的逆变器电路2012年07月08日 560
-
1000米晶体稳频FM立体声发射机2012年07月22日 499