最佳线性滤波理论起源于40年代美国科学家Wiener和前苏联科学家Kолмогоров等人的研究工作,后人统称为维纳滤波理论。从理论上说,维纳滤波的最大缺点是必须用到无限过去的数据,不适用于实时处理。为了克服这一缺点,60年代Kalman把状态空间模型引入滤波理论,并导出了一套递推估计算法,后人称之为卡尔曼滤波理论。卡尔曼滤波是以最小均方误差为估计的最佳准则,来寻求一套递推估计的算法,其基本思想是:采用信号与噪声的状态空间模型,利用前一时刻地估计值和现时刻的观测值来更新对状态变量的估计,求出现时刻的估计值。它适合于实时处理和计算机运算。
现设线性时变系统的离散状态防城和观测方程为:
X(k) = F(k,k-1)·X(k-1)+T(k,k-1)·U(k-1)
Y(k) = H(k)·X(k)+N(k)
其中
X(k)和Y(k)分别是k时刻的状态矢量和观测矢量
F(k,k-1)为状态转移矩阵
U(k)为k时刻动态噪声
T(k,k-1)为系统控制矩阵
H(k)为k时刻观测矩阵
N(k)为k时刻观测噪声
则卡尔曼滤波的算法流程为:
1.预估计X(k)^= F(k,k-1)·X(k-1)
2.计算预估计协方差矩阵
C(k)^=F(k,k-1)×C(k)×F(k,k-1)'+T(k,k-1)×Q(k)×T(k,k-1)'
Q(k) = U(k)×U(k)'
3.计算卡尔曼增益矩阵
K(k) = C(k)^×H(k)'×[H(k)×C(k)^×H(k)'+R(k)]^(-1)
R(k) = N(k)×N(k)'
4.更新估计
X(k)~=X(k)^+K(k)×[Y(k)-H(k)×X(k)^]
5.计算更新后估计协防差矩阵
C(k)~ = [I-K(k)×H(k)]×C(k)^×[I-K(k)×H(k)]'+K(k)×R(k)×K(k)'
X(k+1) = X(k)~
C(k+1) = C(k)~
6.重复以上步骤
-
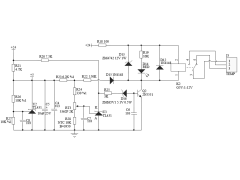
一款高温报警电路2024年11月13日 81
-
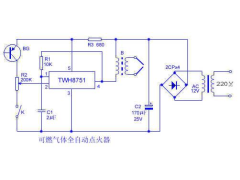
可燃气体全自动点火器2012年09月22日 76
-
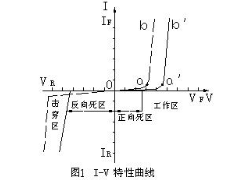
LED参数与特性2012年09月18日 118
-
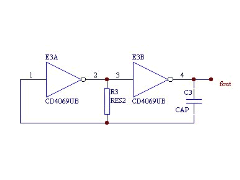
RC振荡电路的几种接法2012年09月10日 221
-
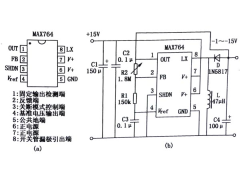
MAX764极性反转电路2012年08月24日 47
-
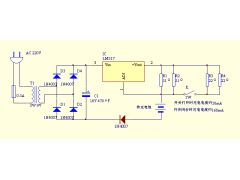
实用恒流充电器2012年08月18日 175
-
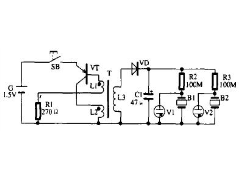
电子催眠器制作2012年08月15日 72
-
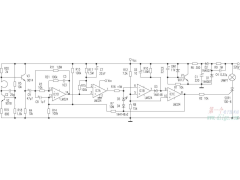
多普勒自动电子开关2012年08月02日 78
-
常用物质金属非金属的电阻率、导电率明细表2024年11月23日 4875
-
自制微型交流电焊机2012年07月14日 1143
-
声光控延时开关的制作2024年07月06日 915
-
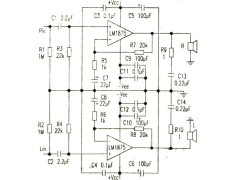
用LM1875替找TDA20302012年09月15日 777
-
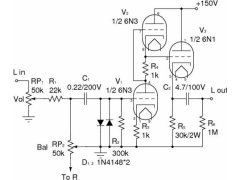
6N3+LM4780功放制作2012年09月13日 653
-
小型太阳能供电板的制作2012年09月08日 649
-
简单的逆变器电路2012年07月08日 560
-
1000米晶体稳频FM立体声发射机2012年07月22日 499