• 状态机代码编写
在大型系统中编码风格会极大的影响状态机的性能。状态机的代码编写方式一般是采用所谓的双always块风格。其一是时序逻辑,在时钟沿到来时将状态向量赋值为下一状态。其二是纯组合逻辑,使用case或if/else语句枚举当前状态和输入可能的组合,并指定下一状态和输出。
但是这并不总是最佳的选择,对于不同的状态机应当具体情况具体分析。下面结合一个例子来说明。实现的功能是“10”序列检测器,相继采样到1,0则输出一个周期的正脉冲,否则一直输出0。该状态机有1个输入:i,1个输出:o。使用Synplify pro 7.6综合,器件选择EPF10K10ATC144-1。
先考虑mealy机。状态图如下:
双always块风格的编码如下:
module test_machine2 (clk, rst_n, i, o);
input clk;
input rst_n;
input i;
output o;
reg o;
reg state;
reg nstate;
parameter S0=1'b0;
parameter S1=1'b1;
always @(posedge clk or negedge rst_n)
if(~rst_n)
state<=S0;
else
state<=nstate;
always @(state or i)
case(state)
S0:
begin
if(i)
nstate<=S1;
else
nstate<=S0;
o<=1'b0;
end
S1:
begin
if(i)
begin
nstate<=S1; o<=1'b0;
end
else
begin
nstate<=S0; o<=1'b1;
end
end
default:
begin
nstate<=S0; o<=1'b0;
end
endcase
endmodule
综合结果:
Total LUTs:2
Register bits:1
Worst Slack:995.595
Estimated Frequency:227.0MHz
前仿真波形:
仿真结果并不理想,因为输出未经同步,其输出时间随输入随时变化。加上输出同步后的代码如下:
reg no;
将组合always块中对o的赋值都替换成对no进行,然后加入:
always @(posedge clk or negedge rst_n)
if(~rst_n)
o<=1'b0;
else
o<=no;
综合后的结果:
Total LUTs:2
Register bits:2
Worst Slack:994.900
Estimated Frequency:196.1MHz
前仿真波形:
而同样功能单always块编码风格的代码如下:
module test_machine (clk, rst_n, i, o);
input clk;
input rst_n;
input i;
output o;
reg o;
reg state;
parameter S0=1'b0;
parameter S1=1'b1;
always @(posedge clk or negedge rst_n)
if(~rst_n)
begin
state<=S0;
o<=1'b0;
end
else case(state)
S0:
begin
if(i)
state<=S1;
else
state<=S0;
o<=1'b0;
end
S1:
begin
if(i)
begin
state<=S1; o<=1'b0;
end
else
begin
state<=S0; o<=1'b1;
end
end
default:
begin
state<=S0; o<=1'b0;
end
endcase
endmodule
其综合结果(系统参数和RTL网表)和仿真波形与增加了输出同步后的双always块编码风格完全相同。
在这个例子中,单always块风格的状态机变量更少,由于将组合逻辑与时序逻辑划分的工作交给综合工具来完成,因此代码在功能上比较简洁清晰。而性能等同于双always块风格的状态机。(当然,在这种小case中也看不出性能能有什么差别来,因此这个结论并不能推广。)
单always还有一个好处,它在仿真效率上略胜一筹。在仿真过程中,单always块状态机仅仅在时钟变化时才需要计算下一状态和输出。而相应的双always块状态机由于有always组合逻辑块,每当输入变化时都要计算下一状态和输出。
那么双always块状态机的优势体现在哪里呢。在大规模状态机中我也作了实验。对1553B总线协议芯片BC模式主状态机,采用两种编码风格综合结果如下(综合工具采用synplify pro 7.2,器件选用EPF10K100ARC240-1,当时没有记录Worst Slack):
|
双always |
单always |
|
|
Total LUTs |
713 of 4992 (14%) |
607 of 4992 (12%) |
|
Register bits |
98 (47 using enable) |
97 (45 using enable) |
|
Estimated Frequency |
75.9MHz |
52.2MHz |
在这个例子中,双always块状态机占用的LUT更多,但是可达频率更高。随着芯片技术的进步,大规模芯片越来越便宜,我们平时更注意的是频率的提高而不是资源的节省。双always块无疑是面积换速度的好方法。
由于以前综合技术的滞后,很多经典文章都推荐双always块编码风格,手动划分组合逻辑与时序逻辑以免综合出垃圾逻辑。而随着技术的进步,将这样的工作交给机器去完成反而可能节约资源,特别是对于新手而言手动划分并不一定可靠时。
双always并不是唯一的选择,对于
1 初学者,为了避免手动划分的失误(很多初学者在预期的组合逻辑中往往综合出锁存器,或者出现例子中输出未同步的现象)
2 可用资源比较苛刻的系统,为了节省资源
3 大型的不追求速度的复杂系统,为了功能级描述的清晰
可以考虑使用单always块风格编写状态机。
以上是对于Mealy机的讨论,下面讨论Moore机。
实现同样的功能,“10”序列检测器,的Moore机状态图如下:
由于Moore机的输出只与当前状态有关,因此实现同样功能的Moore机状态数往往多于Mealy机。
由于输出仅从当前状态组合产生,而下一状态从当前状态和输入共同组合产生。为了清晰,将这两个组合逻辑分开放在不同的always块中。多always块风格的状态机代码如下:
module test_machine4 (clk, rst_n, i, o);
input clk;
input rst_n;
input i;
output o;
reg o;
reg [1:0] state;
reg [1:0] nstate;
parameter S0=2'b00;
parameter S1=2'b01;
parameter S2=2'b10;
always @(posedge clk or negedge rst_n)
if(~rst_n)
state<=S0;
else
state<=nstate;
always @(state)
if(state==S2)
o<=1'b1;
else
o<=1'b0;
always @(state or i)
case(state)
S0:
begin
if(i)
nstate<=S1;
else
nstate<=S0;
end
S1:
begin
if(i)
nstate<=S1;
else
nstate<=S2;
end
S2:
begin
if(i)
nstate<=S1;
else
nstate<=S0;
end
default:
begin
nstate<=S0;
end
endcase
endmodule
单always块风格的状态机编码如下:
module test_machine3 (clk, rst_n, i, o);
input clk;
input rst_n;
input i;
output o;
reg o;
reg [1:0] state;
parameter S0=2'b00;
parameter S1=2'b01;
parameter S2=2'b10;
always @(posedge clk or negedge rst_n)
if(~rst_n)
begin
state<=S0;
o<=1'b0;
end
else case(state)
S0:
begin
if(i)
begin
state<=S1;
o<=1'b0;
end
else
begin
state<=S0;
o<=1'b0;
end
end
S1: // 注意,当前状态(S1)下可以有不同的输出,因为
begin
if(i)
begin
state<=S1;
o<=1'b0; //输出取决于下一状态,而非当前状态
end
else
begin
state<=S2;
o<=1'b1; //输出取决于下一状态,而非当前状态
end
end
S2:
begin
if(i)
begin
state<=S1;
o<=1'b0;
end
else
begin
state<=S0;
o<=1'b0;
end
end
default:
begin
state<=S0;
o<=1'b0;
end
endcase
endmodule
这两者综合后的参数相同:
Total LUTs:2
Register bits:2
Worst Slack:994.900
Estimated Frequency:196.1MHz
其仿真波形也与前面的Mealy机仿真波形一致。
有趣的是两者的RTL图看起来形式不同,实际上对应的门级网表是一样的:
多always块状态机RTL:
单always块状态机RTL:
下面对两者进行比较。
从输出与当前状态对应关系的描述上说,多always块代码的描述更清晰更接近于状态图,而单always块代码则看起来难以理解。这是因为多always块状态机是组合输出,当前状态(state)变化立刻引起输出变化,这一点与状态图相符。而单always块是寄存器输出,当前状态(state)变化后,要等到下一次时钟到来检测到此变化才能引起输出的变化,这导致了输出滞后了一个时钟周期。因此,为了将输出提前,在单always块的Moore机中输出是取决于下一状态而不是当前状态!在例子中,每次状态转移到S2时(state<=S2),必然伴随着输出1(o<=1'b1)。而转移到其他状态时总是输出0。
多always块状态机往往是组合输出。(在这个例子中,由于输出只有1位,并且刚好等于一个状态位,因此在例子中的多always块状态机的输出刚好是直接从寄存器输出。)为了将该输出同步,需要再增加一级寄存器:
reg no;
将组合always块中对o的赋值都替换成对no进行,然后加入:
always @(posedge clk or negedge rst_n)
if(~rst_n)
o<=1'b0;
else
o<=no;
这样不但导致综合输出的逻辑变大,并且输出滞后了一个时钟,如图:
作为总结,对于Moore机,单always块风格代码与状态图的对应较差,难以理解,但能够产生寄存器输出。多always块风格代码清晰易懂,与状态图的对应较好,但通过组合逻辑输出,若再加寄存器同步则会导致输出滞后一个周期。
另一个有趣的现象:Active HDL 6.2根据状态图自动生成的状态机综合出的门级网表(带输出同步),与多always块综合出的门级网表(带输出同步)对比如下(上面是自动生成,下面是手动代码):
• 器件结构
器件结构对于逻辑实现的影响不言而喻。器件结构不但会影响所采用的综合技术,而且也与状态机的状态编码技术互相作用。
早期的器件由二极管、晶体管和简单的门构成。当时使用“状态编码邻接规则”来指导状态的编码和逻辑的化简。具体来说,是用卡诺图表示下一状态和输出函数,通过合并卡诺图中的“1”使得描述FSM组合逻辑部分的乘机项之和表达式中的乘机项最大,而数量最少。(当年我们作数字逻辑试验就干这个,先用卡诺图化简,然后用74系列搭逻辑)。随后技术发生了变化,而上面的原理依然是各种新算法的基础。
PLA出现时期先后有很多逻辑化简和状态编码方法。例如KISS、MAXAD、NOVA等。这些都是基于符号最小化的方法。它们假定逻辑功能采用两层PLA实现,并在这一假定下试图生成最小势的符号覆盖。
多层逻辑器件的出现,使得上面这些方法难以达到优化的效果。由于增加了搜索空间,同时难以构造评价标准,使得符号最小化在多层逻辑领域难以实现。著名的算法例如MUSTANG,它试图使得输出函数表达式中的公共项的数量和大小最大,通过对选定的状态对进行邻接编码分配来完成。
而查找表器件进一步增加了多层逻辑的挑战。在查找表FPGA中,无法使用项和文字的数量来评估功能实现的成本。例如,一个5输入LUT实现一个5输入与门(1个项,5个文字)与实现一个5输入异或门(16个项,80个文字)需要同要的开销。面向FPGA的综合中的特殊工作主要是对输出函数进行并行分解和顺序分解。并行分解是将一个多输出函数分解为多个模块,每个某块可用给定的逻辑块(如4输入1输出LUT)来实现,使得逻辑块的数量最少,逻辑块之间的互联最少。顺序分解是增加特定的过滤模块,将多输入函数的携带信息较少的部分输入进行预处理,产生精简的输出,作为函数逻辑功能的输入。主要算法有基于信息关系与度量的算法、基于语义分析的算法等。
可见,不同的器件类型需要不同的综合方法与之相适应。即使是同一种类的器件,内部结构不同也有不同的综合过程(看那些第三方的综合工具也真够累的),实现性能也有差别。
-
热敏电阻温度阻值查询程序2024年11月13日 74
-
C99语法规则2024年11月16日 675
-
FreeRTOS 动态内存管理2024年11月12日 448
-
一款常用buffer程序2024年11月06日 88
-
1602液晶显示模块的应用2012年08月03日 191
-
GNU C 9条扩展语法2024年11月18日 261
-
如何实现STM32F407单片机的ADC转换2024年11月15日 300
-
STM32使用中断屏蔽寄存器BASEPRI保护临界段2024年11月15日 195
-
C99语法规则2024年11月16日 675
-
51单片机LED16*16点阵滚动显示2012年09月05日 664
-
FreeRTOS 动态内存管理2024年11月12日 448
-
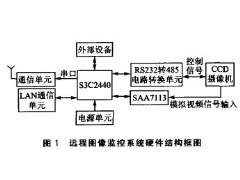
ARM9远程图像无线监控系统2012年07月03日 424
-
用单片机模拟2272软件解码2012年09月06日 300
-
如何实现STM32F407单片机的ADC转换2024年11月15日 300
-
新颖的单片机LED钟2012年08月06日 278
-
GNU C 9条扩展语法2024年11月18日 261